Differentiation

Derivative of Functions of Three Variables 1D 2D Contents

A function f(x,y,z) is differentiable at a point (x₀,y₀,z₀) if there is a well-defined tangent hyperplane at the point (x₀,y₀,z₀,f(x₀,y₀,z₀)), i.e. if there is a linear function plane L(x,y,z) = p(x-x₀) + q(y-y₀) + r(z-z₀) + f(x₀,y₀,z₀) which is closer to the graph than any other hyperplane through the point.

At the end of Section 2, we will develop formal criteria for differentiability, and in the meantime, we will investigate properties that a tangent hyperplane must have.

If there is a well-defined best-approximating hyperplane, then the intersection of that hyperplane with a vertical plane over a line in the domain will be a line which is the tangent line to the slice curve over the line. In particular, for the slice curve (x,y₀,z₀,f(x,y₀,z₀)), the tangent line will lie in the tangent hyperplane, if such a hyperplane exists. The slope of this tangent line is called the x-partial derivative of f at (x₀,y₀,z₀).

Then the x-slope p of the linear function is called the x-derivative of f at (x₀,y₀,z₀) denoted f_x(x₀,y₀,z₀), the y-slope q is called the y-derivative of f at (x₀,y₀,z₀) denoted f_y(x₀,y₀,z₀), and the z-slope r is called the z-derivative of f at (x₀,y₀,z₀) denoted f_z(x₀,y₀,z₀).

Partial Derivatives 2D Cylindrical Coordinates Spherical Coordinates Top of Page Contents

The partial derivatives of a function of three variables are the slopes of the slice curves.

If f(x,y,z) is a function of three variables, then for each y = y₀ and z = z₀, the function f(x,y₀,z₀) is a differentiable function of x, and its derivative is denoted f_x(x₀,y₀,z₀), called the first partial derivative of f with respect to x.

Similarly the derivative of the x = x₀, z = z₀ slice curve f(x₀,y,z₀) with respect to y is denoted by f_y(x₀,y₀,z₀), called the first partial derivative of f with respect to y and the derivative of the x = x₀, y = y₀ slice curve f(x₀,y₀,z) with respect to z is denoted by f_z(x₀,y₀,z₀), called the first partial derivative of f with respect to z.

[D]

Exercises

1. Position the hotspot at the origin. What are the slopes of the tangent lines at this point?

2. Where are the slopes of the tangent lines the greatest for all three slice curves?

Critical Points 1D 2D Cylindrical Coordinates Spherical Coordinates Top of Page Contents

A critical point of a function of two variables f(x,y,z) is a point (x₀,y₀,z₀) such that f_x(x₀,y₀,z₀),= 0, f_y(x₀,y₀,z₀) = 0, and f_z(x₀,y₀,z₀) = 0.

If there is a tangent hyperplane at such a point, then the tangent hyperplane is horizontal.

The x-partial derivative of the function f is itself a function f_x defined over the same domain as f. The collection of points (x,y,z) in the domain such that f_x(x,y,z) = 0 will be the fold set in the x-direction, where the tangent hyperplane, if it exists, is perpendicular to the y-z-w-coordinate hyperplane. Similarly the fold set in the y-direction is the collection of points for which f_y(x,y,z) = 0, where the tangent hyperplane is perpendicular to the x-z-w hyperplane. The fold set in the z-direction is the collection of points for which f_z(x,y,z) = 0, where the tangent hyperplane is perpendicular to the x-y-w hyperplane. The critical points occur at the intersection of the three fold sets in the x-, y-, and z-directions.

We can analyze a function f(x,y) by coloring red all the points in the domain with f_x(x,y) > 0, so that the fold set in the x-direction is the boundary curve of this red set. Similarly the points with f_y(x,y) > 0 can be colored blue, so the fold set in the y-direction is the boundary curve of this blue set. We can then color purple the points where f_x(x,y) > 0 and f_y(x,y) > 0. For almost any critical point, the two fold curves will intersect dividing the plane into four regions, colored red, white, blue and purple, either in clockwise order or counterclockwise order.
If f(x, y, z) is a differentiable function, then (x₀,y₀,z₀) is a critical point of f(x, y, z) if and only if f_x(x₀,y₀,z₀) = f_y(x₀,y₀,z₀) = f_z(x₀,y₀,z₀) = 0.

[D]

Exercises

1. Consider each of the three slice surfaces separately. How does the clockwise order of the coloring relate to the type of critical point found on that slice surface where the four colors meet?

2. If the critical point on the graph of f(x, y, z) is a maximum, what can you say about the critical points on each of the slice surfaces?

3. If the critical point on the graph of f(x, y, z) is a saddle, what can you say about the critical points on each of the slice surfaces?

4. If the critical point on the graph of f(x, y, z) is a minimum, what can you say about the critical points on each of the slice surfaces?

5. In the demo, enter the function f(x, y, z) = x⁴ - 5x²yz + y² + z² and set the hotspot at the point (0, 0, 0). The critical points on all three slices are local minima. Does this mean that the point (0, 0, 0) is a local minimum of the function f(x, y, z)? Why or why not?

Tangent Hyperplanes and Normal Vectors 1D 2D Top of Page Contents

Consider a point P=(x₀,y₀,z₀) in the domain of f(x,y,z). If at this point the xy-, yz-, and xz-slice curves are differentiable, then their tangent lines determine a hyperplane consisting of the points (x₀,y₀,z₀,f(x₀,y₀,z₀)) that is tangent to the hypersurface at P.

This hyperplane is defined as the tangent hyperplane to P and has the equation

w = f_x(x₀,y₀,z₀)(x - x₀) + f_y(x₀,y₀,z₀)(y - y₀) + f_z(x₀,y₀,z₀)(z - z₀) + f(x₀,y₀,z₀).

[D]

Exercises

1. Find equations for the tangent hyperplanes at the point (x₀, y₀, z₀) for each of the following functions:

f(x, y, z) = x² + y² + z²
f(x, y, z) = x + y
f(x, y, z) = xy + 2xz + 3yz
f(x, y, z) = e^x + 2y + sin(z)

2. Describe the xy, xz, and yz slices of the tangent hyperplane at a critical point of a function.

Chain Rule 1D 2D Top of Page Contents

For functions of three variables, there is more than one form of the chain rule.

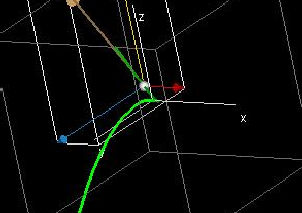
The first example comes when f(x,y,z) is a function of three variables, each of which is a function of t. We then get w(t) = f(x(t),y(t),z(t)) and w’(t) = f_x(x(t),y(t),z(t))x’(t) + f_y(x(t),y(t),z(t))y’(t) + f_z(x(t),y(t),z(t))z’(t) . The curve (x(t),y(t),z(t),w(t)) has tangent vector (x’(t),y’(t),z’(t),w’(t)) lying in the tangent plane to the graph w = f(x,y,z), and this vector projects to the vector (x’(t),y’(t),z’(t),0) in the domain. The vector above (x’(t),0,0,0) in the tangent hyperplane is (x’(t),0,0,f_x(x(t),y(t))x’(t)). Similarly the vector above (0,y’(t),0,0) in the tangent hyperplane is (0,y’(t),0,f_y(x(t),y(t),z(t))y’(t)), and the vector above (0,0,z’(t),0) in the tangent hyperplane is (0,0,z’(t),f_y(x(t),y(t),z(t))z’(t). The vector lying above (x’(t),y’(t),z’(t),0) will then be the sum of these three vectors, i.e. (x’(t),y’(t),z’(t),w’(t)) = (x’(t),0,0,f_x(x(t),y(t))x’(t)) + (0,y’(t),0, f_y(x(t),y(t),z(t))y’(t)) + (0,0,z’(t), f_z(x(t),y(t),z(t))z’(t)) = (x’(t),y’(t),z’(t), f_x(x(t),y(t),z(t))x’(t) + f_y(x(t),y(t),z(t))y’(t)) + f_z(x(t),y(t),z(t))y’(t))).

The tangent line to the graph f(x(t₀),y(t₀),z(t₀)) will then be (x(t₀),y(t₀),z(t₀) + u(x'(t₀),y'(t₀),z'(t₀)). The gradient vector of f at (x₀,y₀,z₀) is defined to be ∇x(t₀),y(t₀),z(t₀) = (f_x(x₀,y₀,z₀),f_y(x₀,y₀,z₀),f_z(x₀,y₀,z₀).

Note that the gradient vector is a vector in the domain of the function. The chain rule can then be written in vector notation as w'(t) = ∇f(x(t),y(t),z(t))⋅(x'(t),y'(t),z'(t)). It follows that the function f(x(t),y(t),z(t)) has a maximum or minimum when the gradient of f at (x(t),y(t)),z(t)) is perpendicular to the velocity vector (x'(t),y'(t),z'(t)) at that point. In particular, if w(t) = c, a constant, then w'(t) = 0 for all t and the velocity vector is perpendicular to the gradient vector at all points.

[D]

Exercises

1. Give a formula for the chain rule for the special case that y(t) and z(t) are constant functions. Do the same for the case that x(t) and z(t) are constant functions and then for the case that x(t) and y(t) are constant functions.

2. Use the chain rule to find the maxima and minima for the function f(x, y, z) = x + y + z along the curve (cos(t), sin(t), cos(2t)).

Differentiability 1D 2D Top of Page Contents

The function f is differentiable at a point (x₀,y₀, z₀) if
lim_{(x,y,z) --> (x0,y0,z0)} |f(x,y,z) - L(x,y,z)|/d((x,y,z), (x₀,y₀,z₀)) = 0
where d((x,y,z), (x₀,y₀,z₀)) = √[(x-x₀)² + (y - y₀)² + (z - z₀)²] is the distance from (x,y,z) to (x₀,y₀,z₀) and L(x, y, z) is the equation for the tangent plane to the function f(x, y, z) at the point (x₀, y₀, z₀).

An alternative definition is that a function f is differentiable at a point p in its domain if there exist functions f_x, f_y, and f_z such that

lim_{h --> 0} |f(p+h) - f(p) - f_x(p)h₁ - f_y(p)h₂ - f_z(p)h₃|/|h| = 0

where h = (h₁,h₂,h₃). This condition can be written in terms of epsilons and deltas as well. We say that f is differentiable at p if for any ε > 0 there exists a δ > 0 such that

|f(p+h) - f(p) - f_x(p)h₁ - f_y(p)h₂ - f_z(p)h₃|/|h| < ε or

-ε|h| + f_x(p)h₁ + f_y(p)h₂ + f_z(p)h₃ < (f(p+h) - f(p)) < ε|h| + f_x(p)h₁ + f_y(p)h₂ + f_z(p)h₃

whenever |h| < δ. This definition of differentiabilty is similar in form to the definition of continuity. Recall that in the geometrical interpretation of continuity the challenge was to find a small enough δ-disc domain at p such that the surface over the domain would lie between two horizontal plates a distance ε above and below f(p). In the geometrical interpretation of differentiability, as seen in the inequality above, the challenge is to find a δ-sphere domain, centered at p, that is small enough so that the surface over the domain lies between two spherical hypercones, where the value of ε determines the slope of the hypercones.

An easier way to visualize this is to consider a slice of the function. For this slice surface, it must be true that the portion of the surface lying over a slice of the spherical domain must lie between two conic slices of the hypercone. This is a way of reducing the problem of differentiability in three dimensions to a problem in two dimensions, which we can understand more easily. The function of three variables will be differentiable at a point if it is differentiable for every slice through that point.

[D]

Exercises

Test whether each function below is differentiable at the specified point:

f(x, y, z) = x² + y² + z², P = (0.5, 0.5, 0.5)
f(x, y, z) = |z|, P = (0, 0, 0)
f(x, y, z) = |z|, P = (0, 0, 0.1)
f(x, y, z) = |x| + |y| + |z|, P = (0, 0, 0)
f(x, y, z) = |x³| + |y³| + |z³|, P = (0, 0, 0)