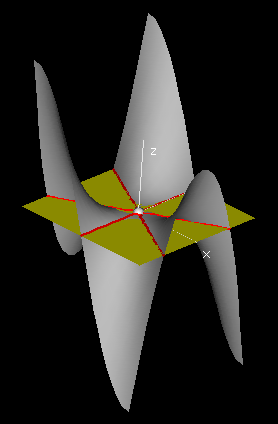
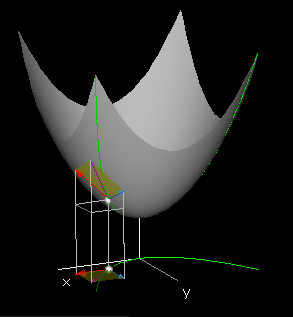
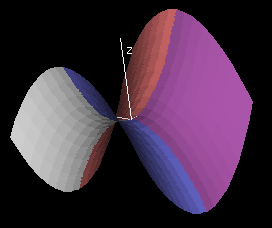Multivariable Calculus

Derivative of Functions of Two Variables 1D 3D Contents

A function f(x,y) is differentiable at a point (x₀,y₀) if there is a well-defined tangent plane at the point (x₀,y₀,f(x₀,y₀)), i.e. if there is a plane L(x,y) = p(x-x₀) + q(y-y₀) + f(x₀,y₀) which is closer to the graph than any other plane through the point.

At the end of Section 2, we will develop formal criteria for differentiability, and in the meantime, we will investigate properties that a tangent plane must have.

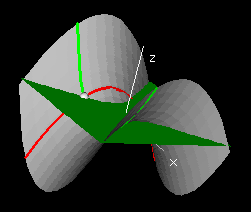
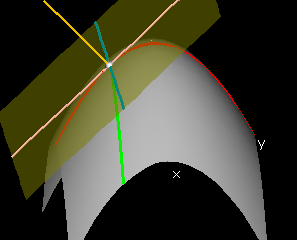
If there is a well-defined best-approximating plane, then the intersection of that plane with a vertical plane over a line in the domain will be a line which is the tangent line to the slice curve over the line. In particular, for the slice curve (x,y₀,f(x,y₀)), the tangent line will lie in the tangent plane, if such a plane exists. The slope of this tangent line is called the x-partial derivative of f at (x₀,y₀), denoted f_x(x₀,y₀).

It follows that f_x(x₀,y₀) is the x-slope p of the linear function L(x,y). It is called the x-derivative of f at (x₀,y₀) or the partial derivative of f with respect to x at (x₀,y₀), denoted f_x(x₀,y₀). Similarly the y-slope q of L(x,y) is called the y-derivative of f at (x₀,y₀) denoted f_y(x₀,y₀).

Partial Derivatives 3D Polar Coordinates Top of Page Contents

The partial derivatives of a function of two variables are the slopes of the slice curves.

For the slice curve y = y₀, given by (x, y₀, f(x,y₀)), the only thing that is changing is the variable x. The derivative of this function with respect to x at x = x₀ is called the "x-partial derivative of f at (x₀,y₀)", denoted f_x(x₀,y₀).

Similarly the derivative with respect to y of the x₀-slice curve (x₀,y,f(x₀,y)) is called the "y-partial derivative of f at (x₀,y₀)" denoted f_y(x₀,y₀).

In terms of the definition of differentiation, f_x(x₀,y₀) is the limit as h goes to zero of the difference quotient (1/h)(f(x₀+h,y₀) - f(x₀,y₀)) and similarly, f_y(x₀,y₀) is the limit as k goes to zero of (1/k)(f(x₀,y₀+k) - f(x₀,y₀)).

[D]

Exercises

Exercise: Find the x- and y-partial derivatives of the following functions at the indicated points.

1. f(x,y) = px + qy + r for constants p, q, and r.

2. f(x,y) = ax² + 2bxy + cy² for constants a, b, and c

3. f(x,y) = x³ - 3xy²

4. f(x,y) = -x⁴ + 2x² - y²

Critical Points of Functions 1D 3D Polar Coordinates Parametric Equations Top of Page Contents

A critical point of a function of two variables f(x,y) is a point (x₀,y₀) such that f_x(x₀,y₀) = 0 and f_y(x₀,y₀) = 0.

If there is a tangent plane at such a point, then the tangent plane is horizontal.

The x-partial derivative of the function f is itself a function f_x defined over the same domain as f. The collection of points (x,y) in the domain such that f_x(x,y) = 0 will be the fold set in the x-direction, where the tangent plane, if it exists, is perpendicular to the y-z-coordinate plane. Similarly the fold set in the y-direction is the collection of points for which f_y(x,y) = 0, where the tangent plane is perpendicular to the x-z-plane. The critical points occur at the intersection of the fold set in the x-direction and the fold set in the y-direction.

[D]

Exercises

Exercises: Find the critical points of the following functions:

1. f(x,y) = x² + 4y² -2x + 4y + 3

2. f(x,y) = x² - 3xy + 2y²

3. f(x,y) = x - xy²

4. f(x,y) = x³ - 3xy²

5. f(x,y) = -x⁴ + 2x² - y²

6. f(x,y) = -(x²+y²)² + 2(x²+y²)

7. f(x,y) = |xy|.

Tangent Planes and Normal Vectors 1D 3D Parametric Equations Polar Coordinates Top of Page Contents

If both partial derivatives of f exist at a point (x₀,y₀), then the equation of the tangent plane of f at (x₀,y₀) is T(x,y) = f(x₀,y₀) + f_x(x₀,y₀)(x - x₀) + f_y(x₀,y₀)(y - y₀).

The tangent line to the slice curve y = y₀ is given by z = f(x₀,y₀) + f_x(x₀,y₀)(x - x₀). In terms of vectors, the tangent line is the line through (x₀,y₀,f(x₀,y₀)) along the vector (1, 0, f_x(x₀,y₀)). We can give this line in parametric form as (x₀,y₀,f(x₀,y₀)) + s(1, 0, f_x(x₀,y₀))

Similarly the tangent line to the slice curve x = x₀ is given by z = f(x₀,y₀) + f_y(x₀,y₀)(y - y₀). In terms of vectors, the tangent line is the line through (x₀,y₀,f(x₀,y₀) along the vector (0, 1, f_y(x₀,y₀)), given parametrically by (x₀,y₀,f(x₀,y₀) + t(0, 1, f_y(x₀,y₀)).

Note that it is easy to find a vector perpendicular both to (1, 0, f_x(x₀,y₀)) and (0, 1, f_y(x₀,y₀)), namely (-f_x(x₀,y₀),-f_y(x₀,y₀),1). The normal line to the graph of f at (x₀,y₀,f(x₀,y₀)) is then given parametrically by (x₀,y₀,f(x₀,y₀) + t(-f_x(x₀,y₀),-f_y(x₀,y₀),1).

[D]

[D]

Exercises

Find the equations of the tangent planes and the normal lines for the following functions at the indicated points.

1. f(x,y) = x² + 4y² -2x + 4y + 3 at (0,0)

2. f(x,y) = x² - 3xy + 2y² at (0,0)

3. f(x,y) = x - xy² at (0,0)

4. f(x,y) = x³ - 3xy² at (0,0)

5. f(x,y) = -x⁴ + 2x² - y² at (0,0), (1,0), and (0,1)

6. f(x,y) = -(x²+y²)² + 2(x²+y²) at (0,0), (1,0), and (0,1)

Chain Rule 1D 3D Polar Coordinates Top of Page Contents

For functions of two variables, there is more than one form of the chain rule.

The first example comes when f(x,y) is a function of two variables, each of which is a function of t. We then get z(t) = f(x(t),y(t)) and z’(t) = f_x(x(t),y(t))x’(t) + f_y(x(t),y(t))y’(t). The curve (x(t),y(t),z(t)) has tangent vector (x’(t),y’(t),z’(t)) lying in the tangent plane to the graph z = f(x,y), and this vector projects to the vector (x’(t),y’(t),0) in the domain. The vector above (x’(t),0,0) in the tangent plane is (x’(t),0,f_x(x(t),y(t))x’(t)) and the vector above (0,y’(t),0) in the tangent plane is (0,y’(t),f_y(x(t),y(t))y’(t)). The vector lying above (x’(t),y’(t),0) will then be the sum of these two vectors, i.e. (x’(t),y’(t),z’(t)) =
(x’(t),0,f_x(x(t),y(t))x’(t)) + (0,y’(t), f_y(x(t),y(t))y’(t)) = (x’(t),y’(t), f_x(x(t),y(t))x’(t) + f_y(x(t),y(t))y’(t))).

[D]

Exercises

How could this demonstration be extended into a proof of the chain rule for two variables?

Find the maximum and minimum values of f(x(t),y(t)) where (x(t),y(t)) = (cos(t),sin(t)), 0 ≤t≤ 2π and f(x,y) = xy.

Same problem for x(t) = cos(t), y(t) = 2sin(t), 0≤t≤2π and f(x,y) = x² + y²

Differentiability 1D 3D Polar Coordinates Top of Page Contents

The function f is differentiable at a point (x₀,y₀) if

lim_{(x,y) --> (x0,y0)} |f(x,y) - L(x,y)|/d((x,y), (x₀,y₀)) = 0

where d((x,y), (x₀,y₀)) = √[(x-x₀)² + (y - y₀)²] is the distance from (x,y) to (x₀,y₀) and L(x, y) is the equation for the tangent plane to the function f(x, y) at the point (x₀, y₀).

[D]

Exercises

Use the demonstrations for continuity and differentiability in two variables to give an argument for why differentiability at a point implies continuity at a point.