« Course List

MA35 Labs

1 Single Variable Calculus

2 » Two Variable Calculus

3 Three Variable Calculus

Polar Coordinate Labs

Two Variable Functions

Contents

2.1 Functions of Two Variables

2.2 Differentiation

2.3 More Derivatives

2.4 Integration

2.5 Vector Analysis

2.5.1 Parametric Curves and Surfaces

2.5.2 Path Integrals

2.5.3 Line Integrals, Circulation, and Flux

2.5.4 Vector Fields, Curl and Divergence

2.5.5 Conservative Vector Fields

2.5.6 Green's Theorem

Search

Path Integrals

Text

If c(t) = (x(t),y(t)) is a path in the plane and f(x,y) is a height function defined over c, then the path integral of f along c is given by ∫_c f(x,y) ds = ∫_a^bf(x(t),y(t))s'(t)dt. where s'(t) = √(x'(t)² + y'(t)²). If f(x,y) = 1 then the path integral is simply the arc length of c.

Demos

Area of a Fence

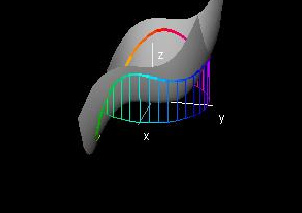
This demonstration calculates the area under a curve on a function graph by approximating the line integral. A function F(x,y) and a curve, written parametrically as C(t) = (x(t),y(t)), are given in the control panel. The 3D graph window shows the function graph (x,y,F(x,y)), the curve C(t) in the domain, and its image F(C(t)) on the graph. The vertical lines along the curve depict the number of partitions used to integrate. The number of partitions can be changed by changing the constant integralRes. The integral is only calculated over C(t), so altering the range of t will affect the value of the integral.

Exercises