|
Second Partial Derivative
Text A second partial derivative is a partial derivative of a function which is itself a partial derivative of another function.
For example, one could take the partial derivative of some function f(x,y) with respect to x, and then take the partial derivative of the resulting function fx(x,y) with respect to y, generating the function fyx(x,y).
There are nine types of second partial derivatives for functions of three variables.
1. fxx(x,y,z) = Partial derivative of fx(x,y,z) with respect to x.
2. fyx(x,y,z) = Partial derivative of fx(x,y,z) with respect to y.
3. fzx(x,y,z) = Partial derivative of fx(x,y,z) with respect to z.
4. fxy(x,y,z) = Partial derivative of fy(x,y,z) with respect to x.
5. fyy(x,y,z) = Partial derivative of fy(x,y,z) with respect to y.
6. fzy(x,y,z) = Partial derivative of fy(x,y,z) with respect to z.
7. fxz(x,y,z) = Partial derivative of fz(x,y,z) with respect to x.
8. fyz(x,y,z) = Partial derivative of fz(x,y,z) with respect to y.
9. fzz(x,y,z) = Partial derivative of fz(x,y,z) with respect to z.
Third, fourth, fifth, and in general, nth partial derivatives for any positive integer n, exist as well.
This is because the progression from first to second partial derivatives can be continued in the same way indefinitely. For example, to get fyzxz(x,y,z), take the partial derivative of fxz(x,y,z) with respect to z, and then take the partial derivative of the result with respect to y.
Demos
Second Partial Derivatives
| 
|
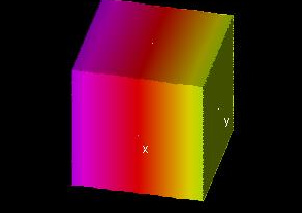
This demo shows graphs of f(x, y, z), one first partial derivative, and one second partial derivative. Red indicates a multiple of 5 (0 in this example). A yellow region next to a red one has a value greater than that multiple of 5, while a magenta region has a lower value.
The demo starts out with the example fzx(x, y, z). To change the first derivative, change g(x, y, z) to f_x(x, y, z), f_y(x, y, z), or f_z(x, y, z). The second derivative, h(x, y, z), will be some derivative of the first derivative with respect to x, y, or z, chosen the same way as before. For example, to see fxy(x, y, z), change g(x, y, z) to f_y(x, y, z) and h(x, y, z) to g_x(x, y, z).
Try changing x0, y0, and z0 to see different layers of these graphs and also to see how their values change as x, y, and z change. (For example, if the second derivative shown is fxy, notice how this second derivative graph describes the changes in fy as you change x0.)
|
Exercises 1. Find the following second partial derivatives as functions of x, y, and z:
- fxz(x, y, z), where f(x, y, z) = x2 + xy + xz
- fyy(x, y, z), where f(x, y, z) = x2yz + xy2z + xyz2
- fzy(x, y, z), where f(x, y, z) = zey
- fxy(x, y, z), where f(x, y, z) = 1/(xyz)
2. Suppose the demo above did not provide graphs of the first and second partial derivatives. How could you use the graph of f(x, y, z) to determine what the graph of fxy(x, y, z) would look like?
3. Consider the function f(x, y, z) = Axy + Bxz + Cyz. Describe the relationships between the mixed second partial derivatives. Will these relationships exist for any function of three variables f(x, y, z) or are there exceptions?
|