|
Parametric Volumes
(Page: 1 | 2
) Text Just as we can use functions of one parameter to generate a curve and functions of two parameters to develop a surface, we can use functions of three parameters to generate a solid.
When we kept one of the parameters constant for parametric surfaces, the result was a parametric curve. This time, were we to keep one parameter constant and allow the other two to vary, the result would be a surface. Keeping two parameters constant would generate a curve. Such a curve would trace out a surface, which in turn would trace out a parametric volume. This process can be extended for any number of variables (volumes trace out objects in 4-space, which trace out objects in 5-space, etc.).
Demos
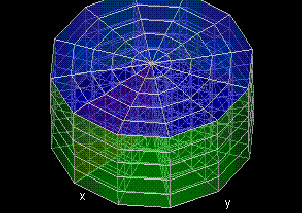
Parametric Volumes

| 
|
This demo allows you to parametrize a volume by defining functions x,y, and z of parameters u, v, and w. By changing a, b, and c, you can see the process by which parametrized surfaces trace out parametrized volumes. 
|
Exercises 1. Parametrize the solid region contained in the irregular tetrahedron whose vertices are (0,0,0), (0,0,1), (1,0,1), and (1, 1, 1).
2. Parametrize a solid sphere of radius 1 centered at the origin.
3. Parametrize a solid torus whose points are distance less than or equal to 1 from a circle of radius 2 in the x-y-plane, centered at the origin.
|