« Course List

MA35 Labs

1 Single Variable Calculus

2 Two Variable Calculus

3 » Three Variable Calculus

Polar Coordinate Labs

Two Variable Functions

Contents

3.1 Functions of Three Variables

3.2 Differentiation

3.2.1 Partial Derivatives

3.2.2 Critical Points

3.2.3 Tangent Hyperplanes and Normal Vectors

3.2.4 Chain Rule

3.2.5 Differentiability

3.3 More Derivatives

3.4 Integration

3.5 Vector Analysis

Search

Partial Derivatives

Text

The partial derivatives of a function of three variables are the slopes of the slice curves. If f(x,y,z) is a function of three variables, then for each y = y₀ and z = z₀, the function f(x,y₀,z₀) is a differentiable function of x, and its derivative is denoted f_x(x₀,y₀,z₀), called the first partial derivative of f with respect to x.

Similarly the derivative of the x = x₀, z = z₀ slice curve f(x₀,y,z₀) with respect to y is denoted by f_y(x₀,y₀,z₀), called the first partial derivative of f with respect to y and the derivative of the x = x₀, y = y₀ slice curve f(x₀,y₀,z) with respect to z is denoted by f_z(x₀,y₀,z₀), called the first partial derivative of f with respect to z.

Demos

Partial Derivatives
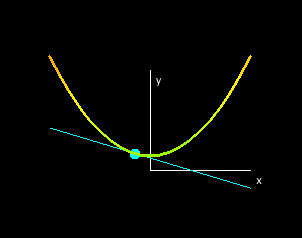
	This demo shows the slice curves at a point (P,f(P)), where P is a point in the domain. The slopes of the slice curves at P give the partial derivatives with respect to x, y and z at (P,f(P)). You can use the hotspot in the "Domain" window to get the partial derivatives of every point in the domain.

Exercises