|
Gauss' Divergence Theorem for Regions between Function Graphs
Text According to Gauss' Divergence Theorem,
∫∫∫W(div F)dV = ∫∫∂WF⋅n)dS.
for some region W in 3-space and its boundary ∂W.
For a proof of Gauss' Divergence Theorem, please expand:

In proving Green's Theorem and Stokes' Theorem, we used the Fundamental Theorem of Calculus to determine how the value of some function changes from one point to another and then used integration to relate some two-dimensional region to its one-dimensional boundary.
We will again use the Fundamental Theorem of Calculus in proving Gauss' Theorem, but this time our result will relate a three-dimensional region to its two-dimensional boundary.
Consider two points (x0, y0, e) and (x0, y0, f) and some function R(x, y, z). From the Fundamental Theorem of Calculus, we know that the difference between R at these two points is given by the integral of Rz from one to the other:
R(x0, y0, f) - R(x0, y0, e) = ∫efRz(x0, y0, z)dz
Now if instead of considering two points, we consider two surfaces e(x, y) and f(x, y) defined for the domain a≤x≤b and c≤y≤d, with e(x, y) ≤ f(x, y), we can relate the values of R on these surfaces by performing a double integral over this domain:
∫cd∫ab(R(x, y, f) - R(x, y, e))dxdy = ∫cd∫ab∫efRz(x, y, z)dzdxdy
Suppose that the function R is the magnitude of the z component of some vector field. The vector form of this component, then, is Rk. It is useful to consider the dot product of this component with the unit normal vector to the surface, Rk⋅n as this represents the flux of the z component of some field across a surface (flux across surfaces is useful, for example, in the study of electric fields).
For pieces dS of surface f(x, y) over some piece of the domain, it turns out that Rk⋅ndS = Rdxdy. In general, for some function g(x, y) the unit normal n is given as (-gx, -gy, 1)/√(gx2 + gy2 + 1). dS is equal to √(gx2 + gy2 + 1)dxdy, so ndS = (-gx, -gy, 1)dxdy. This means that k⋅ndS = (0 * -gx + 0 * -gy + 1 * 1)dxdy = dxdy, so Rk⋅ndS = Rdxdy.
Surface e(x, y) is below surface f(x, y). If we are considering the region in 3-space above surface e(x, y) and below surface f(x, y) and we want the normal to be pointing outward from this region, then the unit normal for e(x, y) must be defined as -1 * (-gx, -gy, 1)/√(gx2 + gy2 + 1). The end result is that, for surface e(x, y), Rk⋅ndS = -Rdxdy.
Now we can make a substitution:
∫∫S1 + S2Rk⋅ndS = ∫∫∫WRz(x, y, z)dV
, where S1 and S2 represent surfaces e(x, y) and f(x, y).
If we want to close the boundary of W with surfaces S3, S4, S5, and S6, we know that these surfaces are all vertical because they are given either constant x or constant y (x = a, x = b, y = c, y = d). This means that the unit normals on these surfaces are perpendicular to k, so
∫∫S3 + S4 + S5 + S6Rk⋅ndS = 0
Now add this to
∫∫S1 + S2Rk⋅ndS = ∫∫∫WRz(x, y, z)dV
to get
∫∫∂WRk⋅ndS = ∫∫∫WRz(x, y, z)dV
Where W is the region in 3-space above e(x, y) and below f(x, y) and ∂W is its boundary.
If Q(x, y, z) is the magnitude of the y component of a vector field and W lies between two functions of x and z, then we can make a similar statement:
∫∫∂WQj⋅ndS = ∫∫∫WQy(x, y, z)dV
Finally, if P(x, y, z) is the magnitude of the x component of a vector field and W lies between two functions of y and z, then:
∫∫∂WPi⋅ndS = ∫∫∫WPx(x, y, z)dV
It turns out that each of the statements above works for limits that are not constants. For example, the first of the three statements would work for a triangular domain. It is thus possible to find certain types of pyramids, triangular prisms, and rectangular prisms which work as regions for all three statements. We can compose any desired region W of infinitesimally small regions of these shapes. This makes the three statements compatible, which means we can add them to get Gauss' Divergence Theorem:
∫∫∫W(div F)dV = ∫∫∂WF⋅n)dS.

Demos
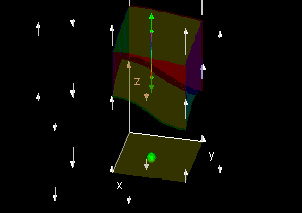
Gauss' Divergence Theorem (RdS term)

| 
|
This demo verifies the statement R(x0, y0, f) - R(x0, y0, e) = ∫efRz(x0, y0, z)dz. You can move the hotspot to different points in the domain to see that the statement is true for the whole domain, which allows us to integrate twice to get ∫cd∫ab(R(x, y, f) - R(x, y, e))dxdy = ∫cd∫ab∫efRz(x, y, z)dzdxdy. 
|
Gauss' Divergence Theorem (QdS term)

| 
|
This demo resembles the first, but instead deals with the statements
Q(x0, d, z0) - Q(x0, c, z0) = ∫cdRz(x0, y, z0)dy and ∫ef∫ab(Q(x, d, z) - Q(x, c, z))dxdz = ∫ef∫ab∫cdQy(x, y, z)dydxdz. 
|
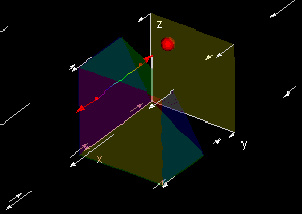
Gauss' Divergence Theorem (PdS term)

| 
|
This demo resembles the first, but instead deals with the statements
P(b, y0, z0) - P(a, y0, z0) = ∫abPx(x, y0, z0)dy and ∫ef∫cd(P(b, y, z) - P(a, y, z))dydz = ∫ef∫cd∫abPx(x, y, z)dxdydz. 
|
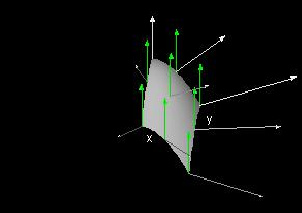
Gauss' Divergence Theorem

| 
|
This demo shows that for some function f(x, y), k⋅ndS = 1 * dxdy, as the vertical component (shown in green) of ndS (shown in white) is always 1. We could make similar statements for functions of x and z and for functions of y and z, and can combine these statements with those illustrated in the previous three demos to get Gauss' Theorem. 
|
Exercises Having seen Green's Theorem applied to divergence in the plane and Gauss' Divergence Theorem, can you make any conjectures regarding divergence in 4 or more dimensions?
|