|
Linear Functions
Text Calculus is the study of functions.
 Functions of three variables are similar in many aspects to those of two variables. One primary difference, however, is that the graphs of functions of more than two variables cannot be visualized directly, as they have dimension greater than three. Instead, slice curves and surfaces, contours and level sets, projections, the gradient vector field and the likes must be used to examine these higher-dimension functions.
Functions of three variables are similar in many aspects to those of two variables. One primary difference, however, is that the graphs of functions of more than two variables cannot be visualized directly, as they have dimension greater than three. Instead, slice curves and surfaces, contours and level sets, projections, the gradient vector field and the likes must be used to examine these higher-dimension functions.

Demos
Linear Functions

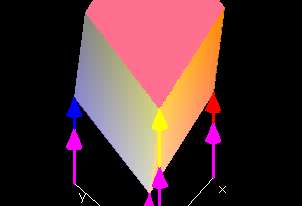
| 
|
This demo shows the linear function in three variables L(x,y,z) = px + qy +k over the rectangular domain 0 ≤ x ≤ 1, 0 ≤ y ≤ 1, 0 ≤ z ≤ 1.
You can change the constants p,q, r and k using the respective red, blue, yellow or magenta slide bar, and the Graph: L(x,y,z) window will show the patch of the function graph of L(x,y,z) with the chosen values for the constants over the rectangular domain.
Note, however, that the function graph is not displayed entirely correctly. In three-dimensional space, it is not possible to display the four mutually perpendicular axeed in the directions of x,y,z and f(x,y,z). Therefore, the fourth axis in f(x,y,z)-direction (indicated by the magenta arrows) is not perpendicular to any of the other directions.
If you slide the hotspot on the purple slidebar, (thereby varying the constant k) the function graph is translated up and down in the directon of f(x,y,z). Varying p,q and r on the red, blue and yellow slidebars will scale in the x-,y- and z-direction of the graph.
Note: For help on using demos, see page 1 of lab 2.1.1. 
|
Examples The Zero Function

The simplest function of all is the zero function, defined by f(x,y,z) = 0 for all x, y, z. This function can be defined for any domain, and the range will always always be the single point { 0 }.

Constant Functions

The next simplest class of functions are the constant functions defined by f(x,y,z) = k for all x, y, z. A constant function can be defined for any domain, and the range will always always be the single point { k }.

Linear Functions

Linear functions are the next most complicated class of functions, defined
by L(x,y,z) = px + qy + rz + k for constants p, q, r, and k. The numbers p, q and r are called the
x-slope, the y-slope, and the z-slope of the linear
function and k is called its w-intercept. The natural domain of the
linear function L is all triples (x,y,z) of real numbers. If p ≠ 0 or q ≠ 0 or r ≠ 0, then the range of L is all real numbers.

Exercises 1. Show that if p ≠ 0, then for every w there is a point (x,y,z) such that L(x,y,z) = px + qy + rz + k = w. Show that if q ≠ 0 or r ≠ 0, then the same result holds.
2. Consider the tetrahedron with vertices at the x-intercept, y-intercept, z-intercept, and w-intercept (i.e. x = y = z = 0) points of the graph of L(x,y,z) = px + qy + rz + k. For what values of p, q, r, and k does this tetrahedron intersect the graph of L(x,y,z) over the domain 0 {leq} x {leq} 1, 0 {leq} y {leq} 1, 0 {leq} z {leq} 1?
|