|
Change of Variables
Text Integration in a non-Cartesian coordinate system requires an application of the Change of Variables Theorem.

Consider what would happen for a function of three variables. Up until now, we have integrated over three variables by adding up the masses of rectangular prisms of density f(x, y, z) and volume dx * dy * dz. If we decide to express x, y, and z as functions of variables u, v, and w, we need to find some new expression for the volume of the differential.
The density will still be the value of the function, expressed as f(x(u,v,w), y(u,v,w), z(u,v,w)).
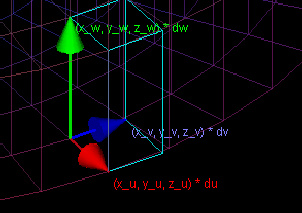
The tiny volume will be a parallelepiped. The three vectors representing the edges of this parallelepiped are based on what happens when u, v, and w change. When u changes by some amount du, x increases by xu*du, y increases by yu*du, and z increases by zu*du. The resulting vector is (xu * du, yu * du, zu*du).
The other two vectors, which are derived similarly, based on what happens when v increases and when w increases, are (xv * dv, yv * dv, zv * dv) and (xw * dw, yw * dw, zw * dw).
To find the volume of this parallelepiped, take the dot product of one edge vector with the cross product of the two other edge vectors. For example, you could take the cross product of the vectors (xv * dv, yv * dv, zv*dv) and (xw * dw, yw * dw, zw*dw):
(yvzw - ywzv, zvxw - zwxv, xvyw - xwyv)dudv.
Now take the dot product of this vector with the remaining
edge vector (xu * du, yu * du, zu * du):
(xu[yvzw - ywzv] + yu[zvxw - zwxv] + zu[xvyw - xwyv])dudvdw.
Finally, multiply by density to get the Change of Variables Theorem for triple integrals:

∫∫∫Df(x, y, z)dxdydz = ∫∫∫D*f(x(u, v, w), y(u, v, w), z(u, v, w))(xu[yvzw - ywzv] + yu[zvxw - zwxv] + zu[xvyw - xwyv])dudvdw,
Where D is the domain in Cartesian coordinates and D* is the domain in the new coordinate system.

Note that the expression
(xu[yvzw - ywzv] + yu[zvxw - zwxv] + zu[xvyw - xwyv])
is equivalent to the determinant of the matrix with rows
(xu, xv, xw), (yu, yv, yw), (zu, zv, zw).

Demos
Change of Variables

| 
|
This demo has three windows. Two of these show the domains in Cartesian coordinates and in the new coordinate system. The third window shows a close-up of the parallelepiped which is used, along with the density function, in integration. 
|
Exercises 1. Find the change of variables formula (i.e. form of
∫∫∫Df(x, y, z)dxdydz = ∫∫∫D*f(x(u, v, w), y(u, v, w), z(u, v, w))(xu[yvzw - ywzv] + yu[zvxw - zwxv] + zu[xvyw - xwyv])dudvdw)
for each of the following coordinate systems:
- x(u, v, w) = (u - v), y(u, v, w) = (u + v), z(u, v, w) = (w + u)
- x(u, v, w) = ucos(v), y(u, v, w) = usin(v), z(u, v, w) = w (cylindrical coordinates)
- x(u, v, w) = ucos(v)cos(w), y(u, v, w) = usin(v)cos(w), z(u, v, w) = sin(w) (spherical coordinates)
2. Under what conditions will the cyan parallelepiped shown in the "D" window have constant volume for all (u, v, w)?
3. How does the change of variables formula for three variables simplify for the case that z = w, and x and y are functions of u and v? Find an example of a situation where this simplification would apply.
|