|
Domain, Range & Function Graphs
(Page: 1 | 2
) Text The domain of a function of two variables is a subset of the
coordinate plane { (x,y) | x,y ∈ R }.

The most common domains
are products of intervals of the form a ≤ x ≤ b, c ≤ y ≤ d.
Another common domain in the plane is a closed disc with center (x0,y0) and radius r given by
 or the open disc where we use less than instead of less than or equal to.
or the open disc where we use less than instead of less than or equal to.

The range of a real-valued function f is the collection of all real numbers f(x,y) where (x,y) is in the domain of f.

The range of the constant function f(x,y) = k is the single number { k }. The range of a linear function L(x,y) = px + qy with p and q not both zero is all real numbers z. The next
simplest functions are linear functions f(x,y) = px + qy + k, where p and q are the partial slopes and k is the z-intercept. The range of this function is all real numbers if p and q are not both zero and just the value { k } if p = 0 = q.

The graph of a function of two variables is the
collection of points (x,y,f(x,y)) in 3-space where (x,y) is in the domain
of f.
 The graph of a linear function of two real variables is a plane
in 3-space.
The graph of a linear function of two real variables is a plane
in 3-space.

Demos
Domain and Range

| 
|
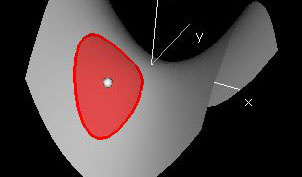
This demonstration graphs a function f(x,y) over a rectangular domain. By default, the domain is set to -1 ≤ x ≤ 1, -1 ≤ y ≤ 1 and the function is set to f(x,y) = x^2 - y^2.
In the window labeled Domain and Range, you can choose both the center and radius of a red disc domain in the xy-plane using the white and red hotspots respectively. The magenta line segment along the z-axis in this window shows the range of f(x,y) over the red disc domain. 
|
Exercises 1. What is the range of the function f(x) = ax2 + cy2? (The answer will depend on the constants a and c.)
2. What is the range of the function f(x,y) = -x4 + 2x2 -y2 where the domain is all (x,y)? (Give reasons for your answer,
without using the words "partial derivative".)
3. What is the range of the function f(x,y) = -x4 + 2x2 - y4 + 2y2?
4. What is the range of the function f(x,y) = x2 + 2bxy + y2? (The answer will depend on the constant b.)
5. What is the range of the function f(x,y) = ax2 + 2bxy + cy2? (The answer will depend on the constants a, b, and c.)
|