|
Domain, Range & Function Graphs
(Page: 1 | 2
) Text Calculus is about functions.
 In multivariable calculus, we begin with real-valued function f that assign a real number f(x,y,z) to each point (x,y,z) in the domain of the function.
In multivariable calculus, we begin with real-valued function f that assign a real number f(x,y,z) to each point (x,y,z) in the domain of the function.

The domain of a function of three variables is a subset of coordinate 3-space \{ (x,y,z) | x, y \mbox{and} z ∈ {R} \}.
 The most common domains are products of intervals of the form a {leq} x {leq} b, c {leq} y {leq} d, e {leq} z {leq} f.
The most common domains are products of intervals of the form a {leq} x {leq} b, c {leq} y {leq} d, e {leq} z {leq} f.

The range of a real-valued function f is the collection of all real numbers f(x,y,z) where (x,y,z) is in the domain of f.
 The simplest example of a function is the constant function that assigns the real number k to all (x,y,z) in the domain. The range of this function is the set { k } containing one point. The next simplest example is a linear function defined by the formula f(x,y,z) = px + qy + rz + k where p, q, and r are the partial
slopes of the linear function and k denotes its
w-intercept.. The range of this function is all real numbers if p, q, and r are not all zero, and just the value { k } if p = 0, q = 0, and r = 0.
The simplest example of a function is the constant function that assigns the real number k to all (x,y,z) in the domain. The range of this function is the set { k } containing one point. The next simplest example is a linear function defined by the formula f(x,y,z) = px + qy + rz + k where p, q, and r are the partial
slopes of the linear function and k denotes its
w-intercept.. The range of this function is all real numbers if p, q, and r are not all zero, and just the value { k } if p = 0, q = 0, and r = 0.

The graph of a function of three variables is the
collection of points (x,y,z,f(x,y,z)) in 4-space where (x,y,z) is in the domain of f.
 As mentioned before, the graph of a function of 3 variables is a 3-dimensional hyperplane lying in 4-space. Therefore the graph cannot be visualized directly; the domain itself is already three dimensional.
As mentioned before, the graph of a function of 3 variables is a 3-dimensional hyperplane lying in 4-space. Therefore the graph cannot be visualized directly; the domain itself is already three dimensional.

Demos
Domain and Range

| 
|
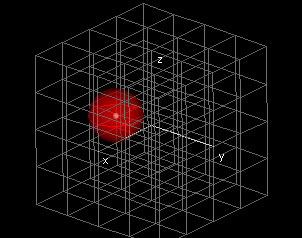
This demonstration shows the three-dimensional domain and the (one-dimensional) range of a function f(x,y,z). By default, the domain is set to -1 {leq} x {leq} 1, -1 {leq} y {leq} 1, -1 {leq} z {leq} 1 and the function is set to f(x,y) = x2 - y2 + z2.
In the window labeled Domain and Range, you can choose both the center and radius of a red spherical domain using the white and red hotspots, respectively. The magenta line segment along the z-axis in this window shows the range of f(x,y,z) of this red domain. 
|
Exercises 1. What is the range of the function f(x,y,z) = ax2 + cy2 + ez2? (The answer will depend on the constants a, c, and e.)
2. What is the range of the function f(x,y,z) = -x4 + 2x2 - y4 + 2y2 - z4 + 2z2 ?
3. In the second demo, whereas every point p in the cube domain -1 {leq} x, y, z {leq} 1 gets assigned a color according to its function value f(p), it is only possible to view the colors that appear on the faces of the cube. When is the range of the colors on the faces the same as the range on the inside of the cube?
4. More generally, what condition has to be satisfied for the range of function values f(p) over a three-dimensional domain to be the same as the range over its boundary?
5. What is the range of the function g(x,y,z) = ax2 + 2bxy + c2 + 2dyz + e2z2 + 2fzx? (The answer will depend on the constants a, b, c, d, e, and f.)
|