|
Continuity
(Page: 1 | 2
| 3
| 4
) Text According to the epsilon-delta definition, a function f of two real variables is said to be continuous at (x0,y0) if for any ε > 0 there exists a &delta such that | f(x,y) - f(x0,y0) | < ε whenever | (x,y) - (x0,y0) | < &delta.
Demos
Continuity

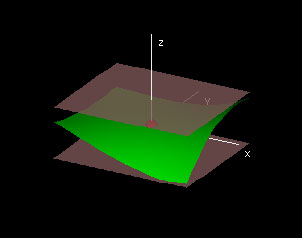
| 
|
This demonstration graphs a function f(x,y) given in Cartesian coordinates, which is a monkey saddle by default. The window labeled "Domain" shows the domain of the grey surface as well as a green disc domain with radius &delta.
The center and "radius" of the green rectangle can be changed by clicking and dragging the red and yellow hotspots respectively. In the graph window, the graph of f(x,y) over this &delta domain is shown in green along with two pink plates a distance ε above and below the red point.
To use this demo to test for continuity, start by choosing an ε in the control panel. The challenge then is to see if it is possible to adjust the radius of the green &delta domain so that the graph over it lies in between the two plates. If it is always possible to find such a delta for any given epsilon, then the function is continuous at that point.

|
Exercises 1. Try using the demo to test the continuity of the following functions at several points, particularly those that you suspect to be points of discontinuity.
f(x, y) = |x| + |y|
2. f(x, y) = |x|/x = |y|/y
3. f(x, y) = x + x3 + y2 + y4
4. f(x, y) = sin(x) + sin(y)
5. f(x, y) = 2xy/(x2+y2)
|