|
Level Sets & Contour Lines
(Page: 1
| 2
| 3 ) Text The collection of all points [r,θ] in the domain of a function f for which f[r,θ] = c is called the level set of f at level c.
 The level set of f is empty if there is no point [r,θ] in the domain of f for which f[r,θ] = c. If [r(t),θ(t)] is a curve in the domain of f such that f[r(t),θ(t)] = c is constant, then the space curve ([r(t),θ(t),c] is called a level curve of f. A plane curve [r(t),θ] in the domain of f such that f[r(t),θ(t)] = c for all t is called a contour.
The level set of f is empty if there is no point [r,θ] in the domain of f for which f[r,θ] = c. If [r(t),θ(t)] is a curve in the domain of f such that f[r(t),θ(t)] = c is constant, then the space curve ([r(t),θ(t),c] is called a level curve of f. A plane curve [r(t),θ] in the domain of f such that f[r(t),θ(t)] = c for all t is called a contour.

Demos
Contour Lines

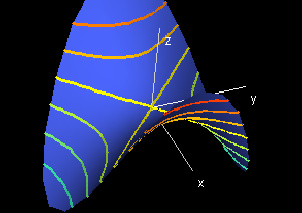
| 
|
This demo shows some level sets for the function f(r,t)= r2cos(2t). The level sets consist of level curves f(r,t) = c, and you can view them on the function graph in the "Function Graph: f(r,t)" window.
In the "Domain" window, we show the level curves projected down into the rt-plane without actually displaying the function graph. This is called a "contour map", and it will prove to be very useful to look at in analyzing function graphs of functions f depending on more than two variables.

|
Exercises Analyze Crater Lake shifted by an earthquake, with function f[r,θ]= -r4 + 2r2 + mrcos(θ) for various values of m. For which m will the lake no longer hold water? Describe the critical levels, i.e. the level sets that contain critical points.
|