« Course List

MA35 Labs

1 Single Variable Calculus

2 » Two Variable Calculus

3 Three Variable Calculus

Polar Coordinate Labs

Two Variable Functions

Contents

2.1 Functions of Two Variables

2.1.1 Introduction

2.1.2 Linear Functions

2.1.3 Domain, Range & Function Graphs

2.1.4 Slice Curves

2.1.5 Level Sets & Contour Lines

2.1.6 Continuity

2.1.7 Normal Vectors for Linear Function Graphs

2.2 Differentiation

2.3 More Derivatives

2.4 Integration

2.5 Vector Analysis

Search

Continuity (Page: 1 | 2 | 3 | 4 )

Text

CONTINUITY IN POLAR COORDINATES

According to the epsilon-delta definition, a function f of two real variables is said to be continuous at (x₀,y₀) if for any ε > 0 there exists a &delta such that | f(x,y) - f(x₀,y₀) | < ε whenever the distance between (x,y) and (x₀,y₀) is less than &delta.

When we are operating in polar coordinates, we may consider x = x₀ + r cos(θ), y = y₀ + r sin(θ), in which case the distance between (x,y) and (x₀,y₀) is | r |. Given any ε > 0, we then have to find a &delta such that | f(x,y) - f(x₀,y₀) | < ε whenever | r | < &delta.

Demos

Continuity

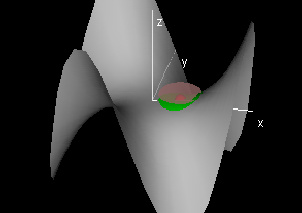
This demonstration graphs a function f[r,θ] given in polar coordinates, which is a monkey saddle by default. The window labeled "Domain" shows the domain of the grey surface as well as a green disc domain with radius &delta. The center and radius of the green disc can be changed by clicking and dragging the red and yellow hotspots respectively. In the graph window, the graph of f[r,θ] over this &delta-domain is shown in green along with two pink plates a distance ε above and below the red point. To use this demo to test for continuity, start by choosing an ε in the control panel. The challenge then is to see if it is possible to adjust the radius of the green &delta domain so that the graph over it lies in between the two plates. If it is always possible to find such a delta for any given epsilon, then the function is continuous at that point.