|
Parametric Curves and Surfaces
(Page: 1
| 2 | 3
) Text PARAMETRIC SURFACES
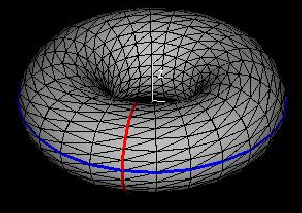
Parametric curves result from expressions for coordinates that depend on one variable. Suppose that these expressions depended instead on two variables, u and v. For a constant value of v, limiting variation to u alone, the resulting graph would be a parametric curve. For a slightly different value of v, the result would be another parametric curve similar to the first, but slightly moved or distorted. Considering all possible values of v, one arrives at a surface which is the set of all possible parametric curves for varying u and constant v.
One could consider parametric curves for varying v and constant u and arrive at the same result.
Demos
Parametric Surfaces

| 
|
This demo portrays the principle discussed above—that one can understand parametric surfaces as two-dimensional objects traced out by one-dimensional parametric curves. The example used is known as a torus.
To see this torus (or any other surface you decide to parametrize) traced out, change a and b using the buttons [<<] and [>>].

|
Exercises Parametrize the following surfaces:
- The square in the x-y plane bounded by the x- and y- axes, the line x = 1, and the line y = 1.
- The triangle in the x-y plane bounded by the x- and y-axes and the line x + y = 1.
- A cylinder (without its bases) of radius 2 and height 2 centered at the origin, with rotational symmetry about the z-axis.
- A sphere of radius 1 centered at the origin.
- A hemisphere of radius 1 centered at the origin, limited to nonnegative x values.
- A “monkey saddle” (z = x^3 – 3xy^2) where x and y are limited to the disk of radius 1 in the x-y plane centered at the origin.
|