« Course List

MA35 Labs

1 Single Variable Calculus

2 Two Variable Calculus

3 » Three Variable Calculus

Polar Coordinate Labs

Two Variable Functions

Contents

3.1 Functions of Three Variables

3.2 Differentiation

3.3 More Derivatives

3.4 Integration

3.5 Vector Analysis

3.5.1 Parametric Volumes

3.5.2 Path Integrals in Three-Space

3.5.3 Vector Fields, Curl and Divergence

3.5.4 Stokes' Theorem for Function Graphs

3.5.5 Conservative Vector Fields

3.5.6 Surface Integrals over Function Graphs

3.5.7 Gauss' Divergence Theorem for Regions between Function Graphs

Search

Vector Fields, Curl and Divergence

Text

In three dimensions, a vector field V can be expressed in terms of the functions p(x,y,z), q(x,y,z), and r(x,y,z) as V(x,y,z) = (p(x,y,z),q(x,y,z),r(x,y,z)). Note that for the gradient vector field, p = f_x, q = f_y, and r = f_z.

The divergence of a three-dimensional vector field V(x,y,z) is defined as div V = ∇ {cdot} V = p_x + q_y + r_z. Note that divergence is a scalar value.

The curl of a three-dimensional vector field V(x,y,z) is defined as curl V = ∇ {times} V = (r_y-q_z, p_z-r_x, q_x-p_y). Note that this is another vector field.

Demos

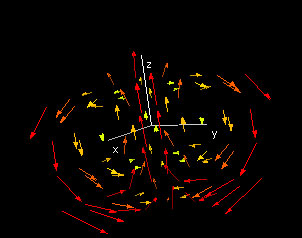
Vector Field with Divergence and Curl

This demo illustrates the curl and the divergence of a three dimensional vector field. You can enter a three-dimensional vector field V by entering the three components p,q and r; the Curl window will the show the curl vector at selected points in the domain. Note that the curl of a vector field is thus a vector field.In the , you can see a color graph of the divergence; each point in the three-dimensional domain is assigned a color based on the value of the divergence of V at that point. The last window color graphs the length of the curl vector at each point.

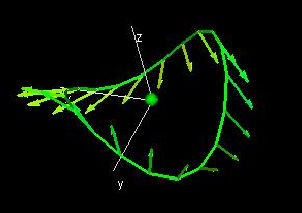
Circulation along a curve in 3D

In this demo, we show the circulation along a curve C(t). The window "The unit tangents" shows the vecor field V(x,y,z) and the curve C(t); the red vectors are the unit tangent at certain points on the curve. The second window, "V(x,y,z) at C(t)" shows the vector field V(x,y) evaluated at (x,y,z)=C(t). In the third window we see a graph of the function that gives the value of the dot product of V(C(t)) with the unit tangent at C(t). The circulation along C(t) is then equal to the (signed) area under the graph, and you can read it off the readout "Circ".

Flux across a surface

In this demo, we show the flux across a surfaceS(t,s). The window "The unit normals" shows the vecor field V(x,y,z) and the surface S; the red vectors are the unit normals at certain points on the surface. The second window, "V(x,y) at C(t)" shows the vector field V(x,y) evaluated at (x,y,z)=S(t,s). In the third window we see the graph of the function that gives the value of the dot product of V(S(t,s)) with the unit normal at S(t,s). The flux across S is then equal to the (signed) volume under the curve, and you can read its value off the readout "Flux".

Exercises