« Course List

MA35 Labs

1 Single Variable Calculus

2 » Two Variable Calculus

3 Three Variable Calculus

Polar Coordinate Labs

Two Variable Functions

Contents

2.1 Functions of Two Variables

2.2 Differentiation

2.3 More Derivatives

2.4 Integration

2.4.1 Volume Under a Function Graph

2.4.2 Riemann Integral

2.4.3 Volume between Function Graphs

2.4.4 Change of Order of Integration

2.4.5 Surface Area for Function Graphs

2.4.6 Change of Variables

2.4.7 Total Mass of a Region in the Plane

2.4.8 Center of Mass

2.4.9 Moment of Inertia

2.5 Vector Analysis

Search

Change of Order of Integration (Page: 1 | 2 )

Text

If we apply Fubini's Theorem to integrals using polar coordinates, we get

∫_a^b∫_c^df(x, y)rdrdθ = ∫_c^d∫_a^bf(x, y)rdθdr = ∫∫_Rf(r, θ)dA

Where dA = dr*dθ.

Demos

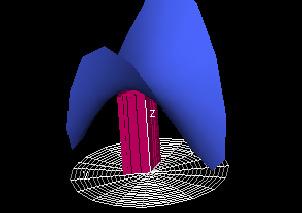
Change of Order of Integration
	In this demo, start with "step" and "step2" set to their minimum values. Increase "step" to its maximum first and then increase "step2" to its maximum to represent integration with respect to r first and θ second. To see the alternative order of integration, increase "step2" first.

Exercises