|
Slice Curves
(Page: 1
| 2
| 3
| 4
| 5 | 6
) Text We begin the study of a function f of two variables r and θ in polar coordinates by fixing one of the variables to produce a function of a single variable defined over an interval.
 If we fix θ = θ0, then the function f(r,θ0), called the slice function over θ = θ0, is a function only of r defined on the interval a {leq} r {leq} b.
Similarly if we fix r = r0, we obtain a function f(r0,θ) of the one variable θ, defined over the interval c {leq} θ {leq} d where 0 {leq} c {leq} d < 2π.
If we fix θ = θ0, then the function f(r,θ0), called the slice function over θ = θ0, is a function only of r defined on the interval a {leq} r {leq} b.
Similarly if we fix r = r0, we obtain a function f(r0,θ) of the one variable θ, defined over the interval c {leq} θ {leq} d where 0 {leq} c {leq} d < 2π.

The collection of points (r,θ0,f(r,θ0)) in the vertical
plane θ = θ0 is the graph of the slice function over θ = θ0, called the slice curve for θ = θ0.
 Similarly the collection of points (r0,θ,f(r0,θ)) in the vertical cylinder r = r0 is called the slice curve for r = r0.
Similarly the collection of points (r0,θ,f(r0,θ)) in the vertical cylinder r = r0 is called the slice curve for r = r0.

Demos
Slice Curves at a Point

| 
|
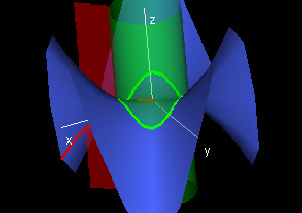
This first demonstration starts with the graph of the function in polar coordinates f(r,t) = r2cos(2t), and it shows the r- and t-slice curves at the orange hot spot P. Moving around the hotspot P=(r0,t0) in the Domain window, observe the two fundamentally different slice curves in the Function Graph: f(r,t) window. The green slice curve is the one determined by f(r0,t) and the red slice curve is determined by f(r,t0).
Note that the green slice curve is the intersection of the green cylinder centered around the z-axis, with radius r0 and the function graph of f, which is depicted in blue. You can view the slice curve all flattened out in the r = r0 window. Furthermore, the red slice f(r,t0) is a ray emanating from the z-axis, and it is the intersection of the red half-plane t = t0 with the graph of the function.

|

| 
|
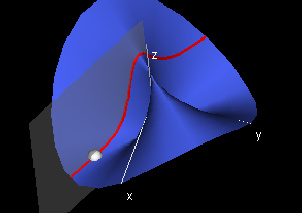
In this demo, use the two hotspots in the Domain window to specify a base point and the direction direction of the slice you want to obtain. The Function Graph: f(r,t) window will then show the slice curve. In this case, the slice curve is the intersection of the horizontal plane through the line specified in the Domain window (grey) with the function graph (blue) in red.

|
|