|
Normal Vectors for Linear Function Graphs
Text A normal vector to a linear function graph is any vector which is perpendicular to that function graph.

One way to find such a vector is to use the fact that two nonzero vectors with a dot product of zero must be perpendicular. If we know three vectors that are parallel to the plane but not parallel to each other, we can find a normal vector by finding a vector whose dot product with each of these three vectors is zero.
For example, for the graph of the function
f(x, y, z) = px + qy + rz + k,
we can choose the vectors (1, 0, 0, p), (0, 1, 0, q), and (0, 0, 1, r) all three of which are parallel to the function graph. For any normal vector N, it must be true that
N⋅(1, 0, 0, p) = 0, N⋅(0, 1, 0, q) = 0, and N⋅(0, 0, 1, r) = 0
This gives us a system of three linear equations for the four components of N, resulting in a range of possibilities. We can add the restriction Nz = 1 and we get
N= (-p, -q, -r, 1).
We can use the same method for the graph of the implicit function
ax + by + cz + dw = e.
Three vectors which are parallel to the graph but not to each other are (d, 0, 0, -a), (0, d, 0, -b), and (0, 0, d, -c).
Again, we have a system of three linear equations for the three components of N. This time, we can add the arbitrary restriction x = a and we get the normal vector (a, b, c, d).

Demos
Normal Vectors for Linear Function Graphs

| 
|
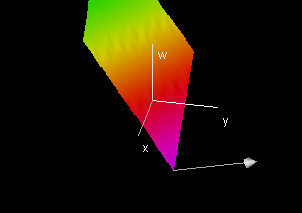
This demo shows the normal vector to the function f(x, y, z) = px + qy + rz + k at the point (x0, y0, z0, f(x0, y0, z0)). The color indicates the value of the w coordinate (function value).
Also displayed are the slice planes of the hyperplane and the normal vectors to those slice planes, which are shadows of the normal vector to the hyperplane. 
|
Normal Vectors for Linear Function Graphs

| 
|
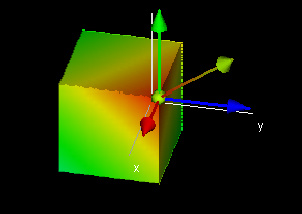
This demo shows the normal vector to the hyperplane defined implicitly by ax + by + cz + dw = e. As above, the color indicates the values of w. The four components of the normal vector are shown as well. Three -- the x, y, and z coordinates -- are shown as arrows (red, blue, and green, respectively). The fourth component, the w component, is shown as a sphere whose color corresponds to the value of w at which the vector (0, 0, 0, d) ends. Note that this color is the same as the color of the tip of the normal vector. 
|
Exercises 1. Find normal vectors for the graphs of the following explicit linear functions:
- f(x, y, z) = 0
- f(x, y, z) = x + y + z
- f(x, y, z) = 3x + y - z
- f(x, y, z) = x +2y - 2z
- f(x, y, z) = z - 2y
2. Find normal vectors for the graphs of the following implicit linear functions:
- x + y + z + w = 1
- x + 2y + 3z + 4w = 1
- x + y = 4
- x - y = 4
- x + y - z - w = 2
- x = 4
- w = 5
3. How does any general expression for the normal vector to a plane depend on k for f(x, y, z) = px + qy + rz + k and e for ax + by + cz + dw = e. Why is this?
|