|
Tangent Planes and Normal Vectors
(Page: 1 | 2
) Text If both partial derivatives of f exist at a point (x0,y0), then the equation of the tangent plane of f at (x0,y0) is L(x,y) = f(x0,y0) + fx(x0,y0)(x - x0) + fy(x0,y0)(y - y0).

The general form of a plane through the point (x0,y0,z0) is L(x,y) = z0 + p(x - x0) + q(y - y0) for appropriate choice of p and q. In order for the tangent lines to the slice curves at (x0,y0) to lie in the tangent plane, we must have p = fx(x0,y0) and q = fy(x0,y0).

The tangent line to the slice curve y = y0 is given by z = z0 + fx(x0,y0)(x - x0). The vector (1, 0, fx(x0,y0)) lies in the direction of the tangent line to the y = y0 slice curve.
 Similarly the vector (0, 1, fy(x0,y0)) is parallel to the tangent line to the x = x0 slice curve. The vector (-fx(x0,y0),-fy(x0,y0),1) is perpendicular to both of these vectors, so it lies along the normal line to the surface at the point. This normal line can be written (x0,y0,z0) + u(-fx(x0,y0),-fy(x0,y0),1).
Similarly the vector (0, 1, fy(x0,y0)) is parallel to the tangent line to the x = x0 slice curve. The vector (-fx(x0,y0),-fy(x0,y0),1) is perpendicular to both of these vectors, so it lies along the normal line to the surface at the point. This normal line can be written (x0,y0,z0) + u(-fx(x0,y0),-fy(x0,y0),1).
The unit vector in the direction of (-fx(x0,y0),-fy(x0,y0),1) is called the unit normal to the graph of f at (x0,y0,z0), written N(x0,y0). Thus N(x0,y0) = (-fx(x0,y0),-fy(x0,y0),1)/√(fx2(x0,y0) + fy2(x0,y0) + 1).

Demos
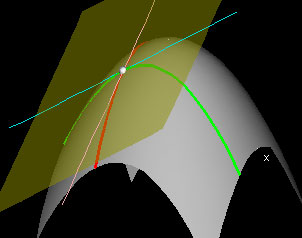
Tangent Plane

| 
|
For this demonstration, choose a point (x0,y0) in the domain using the white hotspot in the window labeled "Domain: f(x,y)". The second window graphs the function f(x,y) and the x- and y-slice curves at the point f(x0,y0). The tangent lines to each of the slice curves at f(x0,y0) are also drawn, and it is clear that together they determine a plane. This plane, which is shown in yellow, is tangent to the graph at f(x0,y0). 
|
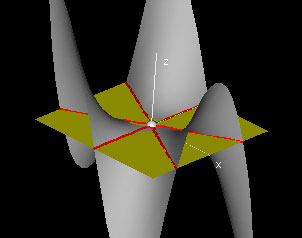
Intersection Set of Tangent Plane

| 
|
This demo shows the tangent planes for the monkey saddle Ax3 - 3Bxy2. Note that the intersection set of the tangent plane with the function graph allows us to classify the points of the surface into two categories: for some points in the domain, the tangent plane meets a neighborhood of the point (x0,y0,f(x0,y0) on the graph in a single point, whereas for other points, the tangent plane meets the graph in a pair of curves, or occasionally in a more complicated set of points. 
|
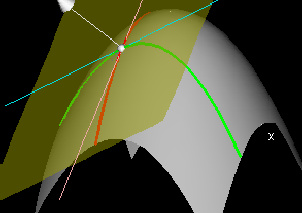
Normal Vectors

| 
|
This demo shows the unit normal vector to the tangent plane for a given point (x0,y0) in the domain. Note that this vector is perpendicular to each of the normal lines drawn to the slice curves. 
|
Exercises 1. Try entering f(x,y) = abs(abs(x) - abs(y)) - abs(x) - abs(y). Using the limit definition of the partial derivatives, show that fx(0,0) = fy(0,0) = 0. Are fx(0,0) and fy(0,0) well-defined? Using the definintion of the tangent plane, show that the tangent plane is z(x,y) = 0. Move the hot spot to the origin. Is the plane z = 0 tangent to the surface? Note that to be tangent to a surface means to touch it at only one point.
2. Which is a stronger condition: the tangent plane exists at a point (x0,y0); or, the partial derivatives are well-defined at a point (x0,y0)?
3. Use the second demo to classify the points of the graphs of the function f(x,y) = Ax2 + 2Bxy + Cy2 for different values of A, B and C.
4. Now change the function f(x,y) in the demo and classify the points of the functions f(x,y) = x2 + y2, g(x,y) = x2 - y2, and h(x,y) = -x4 + 2x2 - y2.
|