|
Chain Rule
Text If (x(t),y(t)) is a differentiable curve in the domain of a differentiable function f, then z(t) = f(x(t),y(t)) is a differentiable function of t and z'(t) = fx(x(t),y(t))x'(t) + fy(x(t),y(t))y'(t).
 The tangent line to the graph of f at f(x(t0),y(t0)) will then be (x(t0),y(t0),z(t0) + u(x'(t0),y'(t0),z'(t0)).
The tangent line to the graph of f at f(x(t0),y(t0)) will then be (x(t0),y(t0),z(t0) + u(x'(t0),y'(t0),z'(t0)).
The gradient vector of f at (x0,y0) is defined to be ∇f(x0,y0) = (fx(x0,y0),fy(x0,y0)).
Note that the gradient vector is a vector in the domain of the function. The chain rule can then be written in vector notation as z'(t) = ∇f(x(t),y(t)) ⋅ (x'(t),y'(t)).
It follows that the function f(x(t),y(t)) has a maximum or minimum when the gradient of f at (x(t),y(t)) is perpendicular to the velocity vector (x'(t),y'(t)) at that point. In particular, if z(t) = c, a constant, then z'(t) = 0 for all t and the velocity vector is perpendicular to the gradient vector at all points.
Every smooth curve (x(t),y(t)) in the domain of a function f determines a curve (x(t),y(t),z(t)) on the graph of the function, where z(t) = f(x(t),y(t)). The velocity vector of this curve at t = t0 will be (x'(t0),y'(t0),z'(t0). If the function f(x,y) has a well-defined tangent plane at the point (x(t0),y(t0), f(x(t0),y(t0)), then the velocity vector of the curve (x(t),y(t),f(x(t),y(t)) at t = t0 will line in the tangent plane. The first two coordinates of this tangent vector will be x'(t0) and y'(t0) so the third coordinate will be z'(t0) = fx(x(t0),y(t0)x'(t0) + fy(x(t0),y(t0)y'(t0). This expression is known as the Chain Rule. Since the same rule will hold at all points of the domain, we can write the Chain Rule as as z'(t) = fx(x(t),y(t))x'(t) + fy(x(t),y(t))y'(t).

Demos
Chain Rule

| 
|
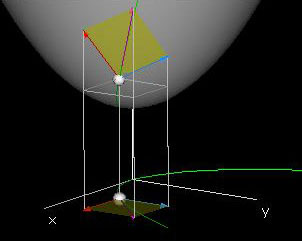
The green curve (x(t),y(t),0) is shown in the horizontal plane (2D graph window). At the point (x(t0),y(t0)) on this curve, three vectors are drawn: the purple tangent vector (x'(t0),y'(t0),0), the red x-component (x'(t0),0,0), and the blue y-component (0,y'(t0),0).
We then introduce a function f(x,y) and show its graph (x,y,f(x,y)) in the 3D graph window. The image of (x(t),y(t)) under f produces a green curve (x(t),y(t),z(t)) that runs along the surface of the graph. The curve (x(t),y(t),z(t)) has its own velocity vector (x'(t),y'(t),z'(t)) = (x'(t),y'(t),fx(x(t),y(t))x'(t) + fy(x(t),y(t))y'(t)) which is given by the chain rule. This tangent vector is drawn at the point z(t0) on the surface as well as its components in the x- and y-directions. Observe that these three vectors are essentially an orthogonal projection of the three vectors in the domain onto the tangent plane at (x(t0),y(t0),f(x(t0),y(t0)). 
|
Exercises How could this demonstration be extended into a proof of the chain rule for two variables?
Find the maximum and minimum values of f(x(t),y(t)) where (x(t),y(t)) = (cos(t),sin(t)), 0 ≤t≤ 2π and f(x,y) = xy.
Same problem for x(t) = cos(t), y(t) = 2sin(t), 0≤t≤2π and f(x,y) = x2 + y2.
|