|
Chain Rule
Text If (x(t),y(t),z(t)) is a differentiable curve in the domain of a differentiable function f, then w(t) = f(x(t),y(t),z(t)) is a differentiable function of t and w'(t) = fx(x(t),y(t),z(t))x'(t) + fy(x(t),y(t),z(t))y'(t) + fz(x(t),y(t),z(t))z'(t).

The tangent line to the graph f(x(t0),y(t0),z(t0)) will then be (x(t0),y(t0),z(t0) + u(x'(t0),y'(t0),z'(t0)). The gradient vector of f at (x0,y0,z0) is defined to be ∇x(t0),y(t0),z(t0) = (fx(x0,y0,z0),fy(x0,y0,z0),fz(x0,y0,z0).
Note that the gradient vector is a vector in the domain of the function. The chain rule can then be written in vector notation as w'(t) = ∇f(x(t),y(t),z(t))⋅(x'(t),y'(t),z'(t)). It follows that the function f(x(t),y(t),z(t)) has a maximum or minimum when the gradient of f at (x(t),y(t)),z(t)) is perpendicular to the velocity vector (x'(t),y'(t),z'(t)) at that point. In particular, if w(t) = c, a constant, then w'(t) = 0 for all t and the velocity vector is perpendicular to the gradient vector at all points.

Demos
Chain Rule

| 
|
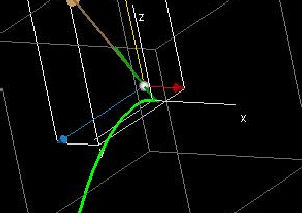
This demo illustrates the Chain Rule for three variables: We have a smooth green curve C given by (x(t),y(t),z(t)) in the three-dimensional domain, and you can use the the tapedeck variable t_0 to specify a point P = (x(t0),y(t0),z(t0)) on the curve. The 3D Graph-Window then shows the tangent vector at P (brown) and the x,y and z-components of the tangent vector. The x-component (x'(t),0,0) is shown in red, the y-component (0,y'(t),0) is shown in blue and the z-component (0,0,z'(t)) is shown in yellow.
The 3D Graph-Window then shows a small part of the curve f(C) = (x(t0),y(t0),z(t0)). (Strictly speaking, the curve would have to lie in four-space.) The point f(P) is shown in grey. The tangent vector at the point f(P) is then shown in brown, with the contributions of the x-,y- and z-components again shown in red, blue and yellow. The three Projection into..-Windows recall how the Chain Rule works in the xy-,xz- and yz-slices, respectively:
For example, take a look at the window titled Projection into the xz-slice. Ignore the z-component for a moment, and recall how we demonstrated the Chain Rule in two dimensions. Then you can see that the contributions from x- and y to the velocity vector at f(P) are given by fx(P)x'(t0) and fy(P)y'(t0), respectively. Likewise, the window titled Projection into the xz-slice, shows that the contributions from x- and z to the velocity vector at f(P) are given by fx(P)x'(t0) and fz(P)z'(t0).
Now a simple argument will show that to get the actual velocity vector at f(P), you just have to add the three distinct contribution from the coordinate components of the curve C, and this shows that the velocity vector at f(P) is given by (x'(t0),y'(t0),z'(t0),fx(P)x'(t0) + fy(P)y'(t0) + fz(P)z'(t0)). 
|
Exercises 1. Give a formula for the chain rule for the special case that y(t) and z(t) are constant functions. Do the same for the case that x(t) and z(t) are constant functions and then for the case that x(t) and y(t) are constant functions.
2. Use the chain rule to find the maxima and minima for the function f(x, y, z) = x + y + z along the curve (cos(t), sin(t), cos(2t)).
|