|
Path Integrals
Text If c(t) = (x(t),y(t)) is a path in the plane and f(x,y) is a height function defined over c, then the path integral of f along c is given by ∫c f(x,y) ds = ∫abf(x(t),y(t))s'(t)dt. where s'(t) = √(x'(t)2 + y'(t)2).
 If f(x,y) = 1 then the path integral is simply the arc length of c.
If f(x,y) = 1 then the path integral is simply the arc length of c.

Demos
Area of a Fence

| 
|
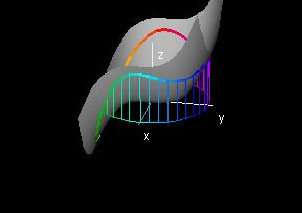
This demonstration calculates the area under a curve on a function graph by approximating the line integral. A function F(x,y) and a curve, written parametrically as C(t) = (x(t),y(t)), are given in the control panel.
The 3D graph window shows the function graph (x,y,F(x,y)), the curve C(t) in the domain, and its image F(C(t)) on the graph. The vertical lines along the curve depict the number of partitions used to integrate. The number of partitions can be changed by changing the constant integralRes. The integral is only calculated over C(t), so altering the range of t will affect the value of the integral. 
|
Exercises 1. While path integrals can be carried out in two-space and three-space, they could still be considered to be part of single variable calculus. Why is this?
2. Find the arc length of the curve (2cos(t), sin(t)), 0 ≤ t ≤ 2π.
|