« Course List

MA35 Labs

1 Single Variable Calculus

2 » Two Variable Calculus

3 Three Variable Calculus

Polar Coordinate Labs

Two Variable Functions

Contents

2.1 Functions of Two Variables

2.2 Differentiation

2.3 More Derivatives

2.4 Integration

2.5 Vector Analysis

2.5.1 Parametric Curves and Surfaces

2.5.2 Path Integrals

2.5.3 Line Integrals, Circulation, and Flux

2.5.4 Vector Fields, Curl and Divergence

2.5.5 Conservative Vector Fields

2.5.6 Green's Theorem

Search

Conservative Vector Fields

Text

A two-dimensional vector field F = (p(x,y),q(x,y)) is conservative if there exists a function f(x,y) such that F = ∇f.

Note that the circulation of ∇f(x,y) along a curve C equals ∫_a^b f_x(x(t),y(t))x'(t) + f_y(x(t),y(t))y'(t) dt = ∫_a^bd/dt(f(x(t),y(t)) dt = f(x(t),y(t))|_a^b = f(x(b),y(b)) - f(x(a),y(a)). In particular, if F(x,y) is a conservative vector field then the circulation of F along a closed curve is 0.

If f exists, then it is called the potential function of F.

If a two-dimensional vector field F(p,q) is conservative, then p_y = q_x.

Suppose that F is conservative and so there does exist a function f such that F = ∇f. Then p = f_x and q = f_y. Now consider the mixed partials f_xy = p_y and f_yx = q_x. By the equality of mixed partials, p_y = f_xy = f_yx = q_x.

If a two-dimensional vector field F(p,q) is conservative, then its curl is identically zero. Since p_y = q_x, ∇ {times} F = (0,0,q_x-p_y) = (0,0,0).

Demos

Conservative Vector Fields

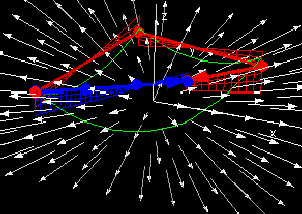
This demo allows you to test whether or not a field is conservative using two piecewise paths, each consisting of three line segments. Use the hotspots in the 2D window to move the endpoints of these line segments. In the 3D window, the wireframes display F⋅ds, and the green curves show the integral of F⋅ds over the two piecewise paths (circulation). You have the option of displaying the graph of some function f(x, y). If (p(x, y), q(x, y)) is the gradient of some function f(x, y) and the red and blue paths are started at the same point, you should be able to find a function graph on which the green curves lie. Two other conditions that will exist for conservative fields: If either the red or the blue curve is a closed curve, the circulation around that curve should be 0 (i.e. the green curve will end up at height 0 at the tip of the arrow, and the area of the wireframe above the x-y plane will equal the area of the wireframe below the x-y plane). If the red and blue curves have the same starting and ending points, then the circulation for each should be equal.

Exercises