|
Green's Theorem
(Page: 1 | 2
) Text Let P(x,y) and Q(x,y) be differentiable functions of x and y. Let D be a region in the plane and let C be the boundary of D. Green's theorem states that
∫C P(x,y) dx + Q(x,y) dy = ∫∫D (- Py(x, y) +Qx(x, y)) dxdy.
where D is the region in the plane bounded by the oriented curve C
Demos
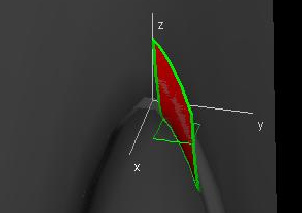
Green's Theorem

| 
|
This demo allows you to test Green's Theorem for rectangles! Use the hotspots in the "V at C(t)" window to move and change the size of the green rectangle. Some of the vectors of the vector field (p(x,y),q(x,y) are shown in the same window, and the "Line Integral" window shows the line integral along the rectangle: It is the volume under the shown graph whose numerical value is given in the readout in the control panel.
Comparing the result with the volume under the function graph of -py+qx, you can see that they are equal. 
|
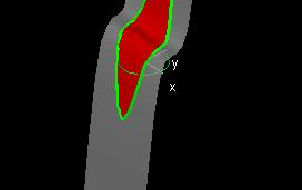
Green's Theorem

| 
|
This demo works the same way as the previous one, except that it tests Green's Theorem for disk-shaped regions. 
|
Exercises 1. Let p(x, y) equal some function of x and let q(x, y) equal some function of y. What is the value of the integral shown at the bottom of the control window? Why does this occur?
2. For either or both of these demos, let p(x, y) = -y and q(x, y) = 0 and observe the properties of the diagrams shown in the different windows. Try changing the size and location of the region. Then do the same for p(x, y) = 0 and q(x, y) = x.
What do you notice in comparing the results of these two trials? What geometric property of the region D is being calculated?
3. In the first demo, Green's theorem for rectangles, try moving the point that starts out as the top-right vertex of the rectangle so that it becomes the top-left vertex. How does the integral change? Why does this change occur?
Now see what happens when the point is the bottom-left vertex or the bottom-right vertex. Explain why this occurs.
|