|
Line Integrals, Circulation, and Flux
Text If C(t) = (x(t),y(t)), α ≤t≤β is a parametrized curve in the plane, then the velocity vector C'(t) is given by C'(t) = x'(t),y'(t)) with length equal to the speed = s'(t) = √(x'(t)2 + y'(t)2). The unit tangent vector is defined to be T(t) = C'(t)/s'(t). and the unit normal vector is defined to be N(t) = (y'(t),-x'(t))/s'(t).
If V = (p(x,y),q(x,y)) is a differentiable vector field in the plane, then the circulation of V along C is defined to be the integral
∫C V⋅T ds = ∫αβ (p(x(t),y(t)),q(x(t),y(t))⋅((x'(t),y'(t))/s'(t))s'(t) dt
= ∫αβ p(x(t),y(t))x'(t) +q(x(t),y(t))y'(t) dt
= ∫C p(x,y)dx + q(x,y)dy.
If V = (p(x,y),q(x,y)) is a differentiable vector field in the plane, then the flux of V across C is defined to be the integral
∫C V⋅N ds = ∫αβ (p(x(t),y(t)),q(x(t),y(t))⋅((y'(t),-x'(t))/s'(t)) s'(t) dt
= ∫αβ p(x(t),y(t))y'(t) -q(x(t),y(t))x'(t) dt
= ∫C- q(x,y)dx.+ p(x,y)dy
Demos
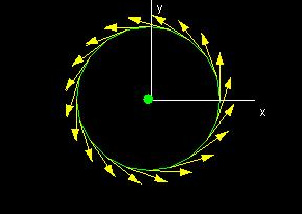
Circulation along C(t)

| 
|
In this demo, we show the circulation along a curve C(t). The window "The unit tangents" shows the vecor field V(x,y) and the curve C(t); the red vectors are the unit tangent at certain points on the curve. The second window, "V(x,y) at C(t)" shows the vector field V(x,y) evaluated at (x,y)=C(t).
In the third window we see a graph of the function that gives the value of the dot product of V(C(t)) with the unit tangent at C(t). The circulation along C(t) is then equal to the (signed) area under the graph, and you can read it off the readout "Circ", 
|
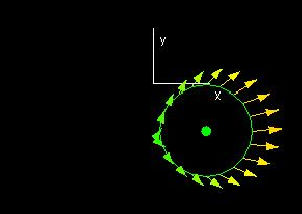
The Flux across C(t)

| 
|
In this demo, we show the flux across a curve C(t). The window "The unit normals" shows the vecor field V(x,y) and the curve C(t); the red vectors are the unit tangent at certain points on the curve. The second window, "V(x,y) at C(t)" shows the vector field V(x,y) evaluated at (x,y)=C(t).
In the third window we see a graph of the function that gives the value of the dot product of V(C(t)) with the unit normal at C(t). The flux across C(t) is then equal to the (signed) area under the curve, and you can read its value off the readout "Flux". 
|
|