Labware - MA35 Multivariable Calculus

The domain of a function of two variables in polar coordinates is a subset of the polar coordinate plane { (r,θ) | r ∈ R \mbox{and} 0 {leq} θ < 2π. The most common domains are products of intervals of the form a {leq} r {leq} b and c {leq} θ {leq} d where 0 {leq} c {leq} d < 2π.
A more general polar coordinate domain is of the form r₁(θ{leq} r {leq} r₂(θ) and c {leq} θ {leq} d where 0 {leq} c {leq} d < 2π.and where 0 ≤ r₁θ) ≤r₂(θ) for two functions r₁ and r₂ of θ.

The range of a real-valued function f is the collection of all real numbers f(p) where p is in the domain of f. The simplest example of a function is the constant function that assigns the real number k to all p in the domain. The range of this function is the set { k } containing one point.

The graph of a function of two variables is the collection of points (x,y,f(x,y)) in 3-space where (x,y) is in the domain of f. When we write the domain in polar coordinates, the graph is said to be in cylindrical coordinates.

Demos

Domain, Range & Function Graphs

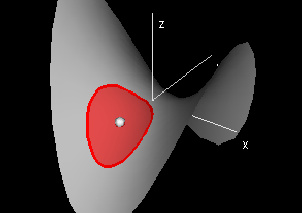
This demonstration graphs a function f[r,θ] over a disc domain. By default, the domain is set to 0 ≤ r ≤ 1, -π ≤ θ ≤ π and the function is set to f[r,θ] = r²cos(2θ). In the window labeled Domain and Range, you can choose both the center and radius of a red disc domain in the xy-plane using the white and red hotspots respectively. The magenta line segment along the z-axis in this window shows the range of f[r.θ] over the red disc domain.

Exercises

What is the range of the function f(x,y) = -x⁴ + 2x² - y² over a unit disc domain centered at the origin (i.e. the set of all points (x,y) such that 0 ≤ r ≤ 1)?

Describe the graph of f(x,y) = 2xy/(x² + y²) for all values of x, y other than (0,0) where the function is not defined.