|
Continuity
(Page: 1
| 2
| 3
| 4 ) Text CONTINUITY IN POLAR COORDINATES
According to the epsilon-delta definition, a function f of two real variables is said to be continuous at (x0,y0) if for any ε > 0 there exists a &delta such that | f(x,y) - f(x0,y0) | < ε whenever the distance between (x,y) and (x0,y0) is less than &delta.
When we are operating in polar coordinates, we may consider x = x0 + r cos(θ), y = y0 + r sin(θ), in which case the distance between (x,y) and (x0,y0) is | r |. Given any ε > 0, we then have to find a &delta such that | f(x,y) - f(x0,y0) | < ε whenever | r | < &delta.
Demos
Continuity

| 
|
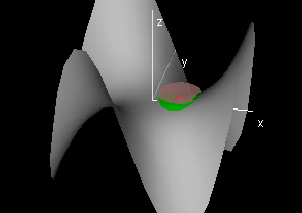
This demonstration graphs a function f[r,θ] given in polar coordinates, which is a monkey saddle by default. The window labeled "Domain" shows the domain of the grey surface as well as a green disc domain with radius &delta.
The center and radius of the green disc can be changed by clicking and dragging the red and yellow hotspots respectively. In the graph window, the graph of f[r,θ] over this &delta-domain is shown in green along with two pink plates a distance ε above and below the red point.
To use this demo to test for continuity, start by choosing an ε in the control panel. The challenge then is to see if it is possible to adjust the radius of the green &delta domain so that the graph over it lies in between the two plates. If it is always possible to find such a delta for any given epsilon, then the function is continuous at that point.

|
|