|
Tangent Hyperplanes and Normal Vectors
Text Consider a point P=(x0,y0,z0) in the domain of f(x,y,z).
If at this point the xy-, yz-, and xz-slice curves are differentiable, then their tangent lines determine a hyperplane consisting of the points (x0,y0,z0,f(x0,y0,z0)) that is tangent to the hypersurface at P.

This hyperplane is defined as the tangent hyperplane to P and has the equation
w = fx(x0,y0,z0)(x - x0) + fy(x0,y0,z0)(y - y0) + fz(x0,y0,z0)(z - z0) + f(x0,y0,z0).

Demos
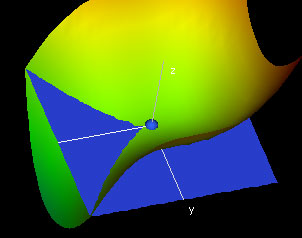
Slicing the Tangent Hyperplane

| 
|
In this demo, we show some slices of the tangent hyperplane at a point P on a function graph of three variables.
We slice the tangent plane in the direction of the coordinate axes at the hotspot P (in blue), which you can move around in the Domain-Window. In the Slices-Window you can see the colored slice surfaces of the function graph at the point . As usual, the color of the slice corresponds to the value of f(x,y,z).
The slice surfaces are then displayed as function graphs in the XY-, YZ- and XZ- Slices Windows, together with the slices of the tangent hyperplane. Note that the slices of the tangent hyperplane are the tangent planes of the slices(Why?). 
|
Exercises 1. Find equations for the tangent hyperplanes at the point (x0, y0, z0) for each of the following functions:
- f(x, y, z) = x2 + y2 + z2
- f(x, y, z) = x + y
- f(x, y, z) = xy + 2xz + 3yz
- f(x, y, z) = ex + 2y + sin(z)
2. Describe the xy, xz, and yz slices of the tangent hyperplane at a critical point of a function.
|