|
Tangent Planes and Normal Vectors
(Page: 1
| 2 ) Text If both partial derivatives for each coordinate function of the parametrized surface (x(u,v), y(u,v), z(u,v)) exist at a point (u0,v0), then the tangent plane of the surface at (u0,v0) is the plane determined by the vectors
(xu(u0,v0), yu(u0,v0), zu(u0,v0)) and
(xv(u0,v0), yv(u0,v0), zv(u0,v0)).
The unit normal to the point (x(u0,v0), y(u0,v0), z(u0,v0)) is the cross product of the two vectors above divided by this cross product's magnitude.
Demos
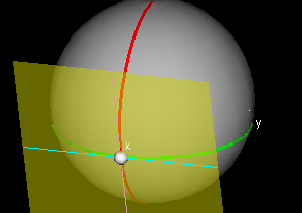
Tangent Plane to a Parametrized Surface

| 
|
For this demonstration, choose a point (u0,v0) in the domain. You will see a graph of the parametrized surface (x(u,v), y(u,v), z(u,v)) and the u- and v-slice curves at the point (x(u0,v0), y(u0,v0), z(u0,v0)). The tangent lines to each of the slice curves at (x(u0,v0), y(u0,v0), z(u0,v0)) are also drawn, and it is clear that together they determine a plane. This plane, which is shown in yellow, is tangent to the graph at (x(u0,v0), y(u0,v0), z(u0,v0)).

|
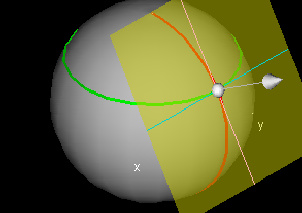
Normal Vector to a Parametrized Surface

| 
|
This demo shows the unit normal vector to the tangent plane for a given point (u0,v0) in the domain. 
|
|