|
Constrained Maxima & Minima
Text Given a contour g(x,y,z) = c of a function g, we can find the maximum value of the function f(x,y,z) on this contour by locating the points at which a contour of f is tangent to the contour of g.
At such a point the gradient of f is parallel to the gradient of g, such that
∇f(x,y,z) = λ∇g(x,y,z)
where λ is constant.

This leads to the system of equations
fx(x,y,z) = λgx(x,y,z)
fy(x,y,z) = λgy(x,y,z)
fz(x,y,z) = λgz(x,y,z)
g(x,y,z) = c.
Any points (x,y,z) which satisfy this system are the critical points of the function f restricted to the contour g(x,y,z) = c.

Demos
Constrained Maxima and Minima

| 
|
This demo shows the level set for g(x, y, z) = c as well as the level set for f(x, y, z) at some value l, which you can change. Maximum and minimum values of f(x, y, z) on the surface g(x, y, z) = c occur where this surface is tangent to one of the level sets of f(x, y, z).
Note: This demo may take a minute or two to load. 
|
Constrained Maxima and Minima

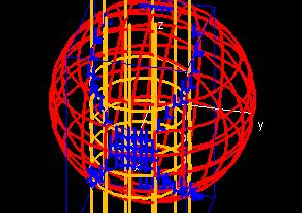
| 
|
This demo is a copy of the one above with the additional feature of displaying intersection points. Use the hotspots to select the region you would like to test for intersection points, and then search through the intersection points to see if any of them are points of tangency. 
|
Constrained Maxima and Minima

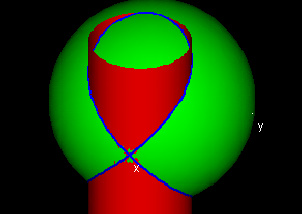
| 
|
This demo provides a clearer picture of the example used in the previous two demos. It is not designed to work with any other examples. 
|
Exercises 1. Find the maximum and minimum values of x2 + y2 + z2 on the surface (x - 0.5)2 + y2 = 0.52.
2. Find the maximum and minimum values of cos(x) + cos(x) - z on the surface z = 2.
3. Find the maximum and minimum values of cos(x) + cos(x) - z on the surface x2+y2+z2 = 1.
|