|
Slice Curves
(Page: 1
| 2 | 3
| 4
| 5
| 6
) Text We can generalize slice curves by considering the slice above any line (y - y0) = m(x - x0).
Demos
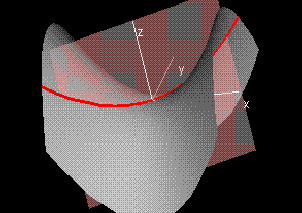
Slice Curve along a Line

| 
|
This second demonstration is a generalization of the first in that it allows you to choose an arbitrary line (y - y0) = m(x - x0) in the domain window. The two orange hotspots control the location of the point (x0,y0) and the direction of the line. The graphs of the surface (x,y,f(x,y)) as well as the image of the line under f are shown in a separate window. A pink slicing plane has also been added. 
|
Exercises 1. Analyze the slices of the general quadratic function f(x,y) = Ax2 + 2Bxy + Cy2 for various values of A, B, and C. For which A, B, and C will the range consist of all real numbers? All non-negative numbers? All non-positive numbers?
2. Analyze the function f(x,y) = x2*y/(x4 + y2) for (x,y) ≠ (0,0) and f(0,0) = 0. What can be said about the restriction of this funciton to a line y = mx through the origin? What is the range of this function, and at what points will the maximum value be taken on?
|