« Course List

MA35 Labs

1 Single Variable Calculus

2 » Two Variable Calculus

3 Three Variable Calculus

Polar Coordinate Labs

Two Variable Functions

Contents

2.1 Functions of Two Variables

2.1.1 Introduction

2.1.2 Linear Functions

2.1.3 Domain, Range & Function Graphs

2.1.4 Slice Curves

2.1.5 Level Sets & Contour Lines

2.1.6 Continuity

2.1.7 Normal Vectors for Linear Function Graphs

2.2 Differentiation

2.3 More Derivatives

2.4 Integration

2.5 Vector Analysis

Search

Level Sets & Contour Lines (Page: 1 | 2 | 3 )

Text

The collection of all points [r,θ] in the domain of a function f for which f[r,θ] = c is called the level set of f at level c. The level set of f is empty if there is no point [r,θ] in the domain of f for which f[r,θ] = c. If [r(t),θ(t)] is a curve in the domain of f such that f[r(t),θ(t)] = c is constant, then the space curve ([r(t),θ(t),c] is called a level curve of f. A plane curve [r(t),θ] in the domain of f such that f[r(t),θ(t)] = c for all t is called a contour.

Demos

Contour Lines

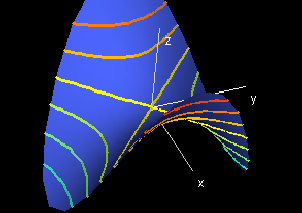
This demo shows some level sets for the function f(r,t)= r2cos(2t). The level sets consist of level curves f(r,t) = c, and you can view them on the function graph in the "Function Graph: f(r,t)" window. In the "Domain" window, we show the level curves projected down into the rt-plane without actually displaying the function graph. This is called a "contour map", and it will prove to be very useful to look at in analyzing function graphs of functions f depending on more than two variables.

Exercises